Page 17 - vol2

5. példa: Egy 30 cm oldalú négyzet négy
sarkából vágjunk le négy egybevágó
négyzetet úgy, hogy a lap négy szélének a
felhajtásával a lehető legnagyobb
térfogatú dobozt kapjunk! Adjuk meg
ennek a térfogatát!
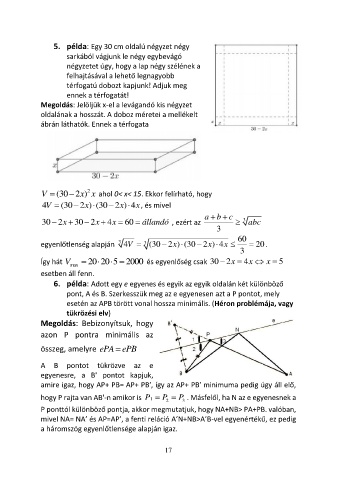
Megoldás: Jelöljük x-el a levágandó kis négyzet
oldalának a hosszát. A doboz méretei a mellékelt
ábrán láthatók. Ennek a térfogata

−
V = (30 2 ) x ahol 0< x< 15. Ekkor felírható, hogy
2
x
−

−

4V = (30 2 ) (30 2 ) 4x, és mivel
x
x
+
+
a b c
−
30 2x + 30 2x + 4x = 60 = állandó , ezért az  3 abc
−
3
60
−

−

egyenlőtlenség alapján 4V = 3 (30 2 ) (30 2 ) 4x  = 20 .
3
x
x
3
=


Így hát V max = 20 20 5 2000 és egyenlőség csak 30 2x− = 4x  =
5
x
esetben áll fenn.
6. példa: Adott egy e egyenes és egyik az egyik oldalán két különböző
pont, A és B. Szerkesszük meg az e egyenesen azt a P pontot, mely
esetén az APB törött vonal hossza minimális. (Héron problémája, vagy
tükrözési elv)
Megoldás: Bebizonyítsuk, hogy
azon P pontra minimális az
összeg, amelyre ePA ePB=
A B pontot tükrözve az e
egyenesre, a B' pontot kapjuk,
amire igaz, hogy AP+ PB= AP+ PB′, így az AP+ PB′ minimuma pedig úgy áll elő,
hogy P rajta van AB'-n amikor is P = 1 P = 2 P . Másfelől, ha N az e egyenesnek a
3
P ponttól különböző pontja, akkor megmutatjuk, hogy NA+NB> PA+PB. valóban,
mivel NA= NA’ és AP=AP’, a fenti reláció A’N+NB>A’B-vel egyenértékű, ez pedig
a háromszög egyenlőtlensége alapján igaz.

17