Page 20 - vol2

12. példa: Adott az ABC háromszög és síkjában az e egyenes. Keressük
2
az e egyenes azon P pontját, amelyre PA + 2 PB + 2 PC minimális!
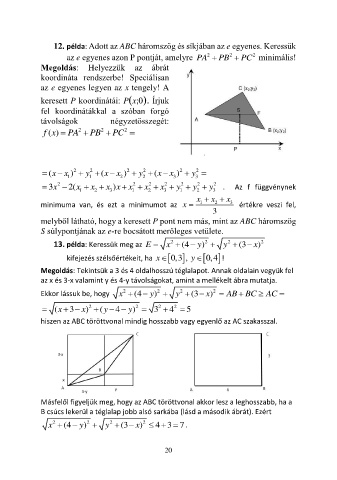
Megoldás: Helyezzük az ábrát
koordináta rendszerbe! Speciálisan
az e egyenes legyen az x tengely! A

keresett P koordinátái: P(x;0) Írjuk
fel koordinátákkal a szóban forgó
távolságok négyzetösszegét:
2
=
f ( ) PA + 2 PB + 2 PC =
x

2
2
−
2
2
2
−
2
−
= (x x 1 ) + y + (x x 2 ) + y + (x x 3 ) + y =
2
1
3
2
2
+
2
2
2
= 3x − 2(x + x + x 3 )x x + x + x + y + y + y . Az f függvénynek
2
2
1
1
3
3
2
2
1
2
x + x + x
minimuma van, és ezt a minimumot az x = 1 2 3 értékre veszi fel,
3
melyből látható, hogy a keresett P pont nem más, mint az ABC háromszög
S súlypontjának az e-re bocsátott merőleges vetülete.
−
−
13. példa: Keressük meg az E = x + (4 y ) + y + (3 x )
2
2
2
2

kifejezés szélsőértékeit, ha x 0,3 y , 0,4 !
Megoldás: Tekintsük a 3 és 4 oldalhosszú téglalapot. Annak oldalain vegyük fel
az x és 3-x valamint y és 4-y távolságokat, amint a mellékelt ábra mutatja.
Ekkor lássuk be, hogy x + (4 y ) + y + (3 x ) = AB BC  AC =
+
−
−
2
2
2
2
2
2
2
−
2
= (x + 3 x + (y − 4 y ) = 3 + 4 =
−
5
)
hiszen az ABC töröttvonal mindig hosszabb vagy egyenlő az AC szakasszal.

Másfelől figyeljük meg, hogy az ABC töröttvonal akkor lesz a leghosszabb, ha a
B csúcs lekerül a téglalap jobb alsó sarkába (lásd a második ábrát). Ezért
−
2
x + (4 y ) + y + (3 x )  4 3 7 .
2
2
+
=
−
2

20