Page 67 - vol2

és ezzel megoldottuk a feladatot.

b
4. feladat: Ha a , ,c pozitív valós számok amelyekre a b c+ + = 1,
−
+
+
−
+
−
(b c a ) 2 (c a b ) 2 (a b c ) 2 3
igazoljuk, hogy + +  .
(b c + a 2 (c a + b 2 (a b + c 2 5
2
+
+
+
2
2
)
)
)
Megoldás: Mivel a b c+ + = 1, ezért a bizonyítandó egyenlőtlenség így
−
−
−
a
c
(1 2 ) 2 (1 2 ) 2 (1 2 ) 2 3
b
alakul: + +  . De
−
−
a + (1 a ) 2 b + (1 b ) 2 c + (1 c ) 2 5
−
2
2
2
−
(1 2 ) 2 = 2− 2
a
a + (1 a ) 2 1 (1 2 ) 2 , ezért célszerűnek látszik bevezetni
+
−
−
2
a
)
−
−
=
−
+
+
−
x = 1 2 , y = 1 2 , z = 1 2c így x y z = 3 2 1 és , ,x y z  (0,1
a
b
1 1 1 27
továbbá bizonyítani kell, hogy + +  .
+
+
+
1 x 2 1 y 2 1 z 2 10
1
)
Tekintsük az f ( ) = , f ( : 0,1 → R függvényt. Mivel f "( ) nem
t
t
+
1 t 2
)
előjeltartó a (0,1 intervallumon, ezért sem nem konvex, sem nem
1
konkáv. Mivel a b c+ + = 1 fennáll ha a b c= = = ezért felírjuk az érintő
3
 1  1    1   1   1 

egyenletét az  , f    belső pontban: y − f   = ' f    x − 
 3  3    3   3   3 
−
27(2 x )
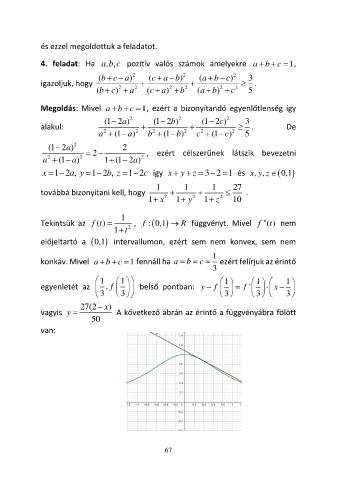
vagyis y = A kővetkező ábrán az érintő a függvényábra fölött
50
van:

67