Page 62 - vol2
P. 62
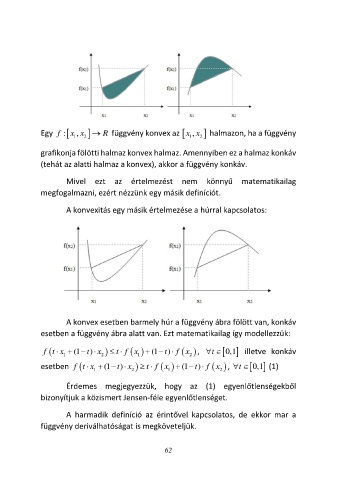
Egy f : x x → R függvény konvex az , x halmazon, ha a függvény
,
x
2
1
1
2
grafikonja fölötti halmaz konvex halmaz. Amennyiben ez a halmaz konkáv
(tehát az alatti halmaz a konvex), akkor a függvény konkáv.
Mivel ezt az értelmezést nem könnyű matematikailag
megfogalmazni, ezért nézzünk egy másik definíciót.
A konvexitás egy másik értelmezése a húrral kapcsolatos:
A konvex esetben barmely húr a függvény ábra fölött van, konkáv
esetben a függvény ábra alatt van. Ezt matematikailag így modellezzük:
( f t x 1 + (1 t x 2 ) t f ( ) (1x + − ) t f x 2 t illetve konkáv
( ) ,
−
0,1
)
1
( ) , t
−
esetben ( f t x 1 + (1 t x 2 ) t f ( ) (1x + − ) t f x 2 (1)
0,1
)
1
Érdemes megjegyezzük, hogy az (1) egyenlőtlenségekből
bizonyítjuk a közismert Jensen-féle egyenlőtlenséget.
A harmadik definíció az érintővel kapcsolatos, de ekkor mar a
függvény deriválhatóságat is megköveteljük.
62