Page 63 - vol2

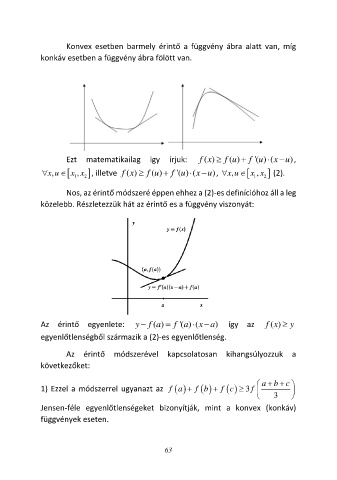
Konvex esetben barmely érintő a függvény ábra alatt van, míg
konkáv esetben a függvény ábra fölött van.


−
u
x
)
u
Ezt matematikailag igy írjuk: f ( )  f ( )+ f '( ) (x u ,


−

 , x u   ,x x , illetve ( )f x  f ( )+ f '( ) (x u , x ) ,u   ,x x (2).
u
u
1
2
1
2
Nos, az érintő módszeré éppen ehhez a (2)-es definícióhoz áll a leg
közelebb. Részletezzük hát az érintő es a függvény viszonyát:

−
Az érintő egyenlete: y − f ( ) = f '( ) (x a így az f ( ) 

a
y
x
a
)
egyenlőtlenségből származik a (2)-es egyenlőtlenség.
Az érintő módszerével kapcsolatosan kihangsúlyozzuk a
következőket:
a b c  +  +
1) Ezzel a módszerrel ugyanazt az ( ) a + f ( ) b + f ( ) 3c  f  
f
 3 
Jensen-féle egyenlőtlenségeket bizonyítják, mint a konvex (konkáv)
függvények eseten.

63