Page 65 - vol2

1 5  1  5x − 1
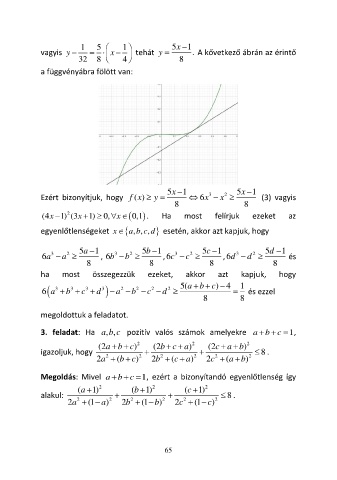
vagyis y − =   x −  tehát y = . A kővetkező ábrán az érintő
32 8  4  8

a függvényábra fölött van:

5x − 1 5x − 1
3
2
x
Ezért bizonyítjuk, hogy f ( )  =  6x − x  (3) vagyis
y
8 8
)
2

(4x − 1) (3x + 1)  0, x (0,1 . Ha most felírjuk ezeket az

egyenlőtlenségeket x  , , ,a b c d esetén, akkor azt kapjuk, hogy
5a − 1 5b − 1 5c − 1 5d − 1
6a − 3 a  2 , 6b − 3 b  2 ,6c − 3 c  2 ,6d − 3 d  2 és
8 8 8 8
ha most összegezzük ezeket, akkor azt kapjuk, hogy
+
−
+
5(a b c ) 4 1
2
2
2
3
3
( 6 a + b + c + d 3 ) a− 2 − b − c − d  = és ezzel
3
8 8
megoldottuk a feladatot.
3. feladat: Ha , ,a b c pozitív valós számok amelyekre a b c+ + = 1,
+
+
+
+
+
+
(2a b c ) 2 (2b c a ) 2 (2c a b ) 2
igazoljuk, hogy + +  8 .
+
2a + (b c ) 2 2b + (c a ) 2 2c + (a b ) 2
+
+
2
2
2
Megoldás: Mivel a b c+ + = 1, ezért a bizonyítandó egyenlőtlenség így
(a + 1) 2 (b + 1) 2 (c + 1) 2
alakul: + +  8 .
2a + (1 a ) 2 2b + (1 b ) 2 2c + (1 c ) 2
2
2
−
−
2
−

65