Page 33 - vol1

Ugyanakkor a matematikában egy újabb művelet jelent meg, a hatványozás.
=
Jelen esetben a a : a , és az a -t négyzetszámnak vagy teljes négyzetnek
2
2
nevezzük (itt a * ). Az n-edik négyzetszám képlete: N = n 2 , n  * .
n
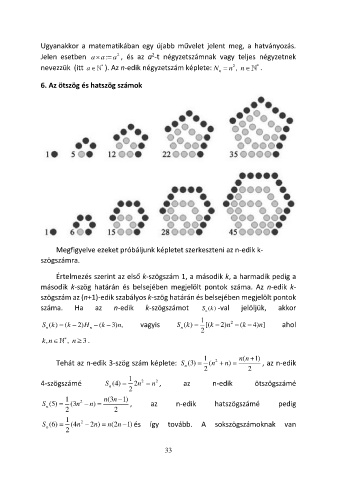
6. Az ötszög és hatszög számok

Megfigyelve ezeket próbáljunk képletet szerkeszteni az n-edik k-
szögszámra.

Értelmezés szerint az első k-szögszám 1, a második k, a harmadik pedig a
második k-szög határán és belsejében megjelölt pontok száma. Az n-edik k-
szögszám az (n+1)-edik szabályos k-szög határán és belsejében megjelölt pontok
száma. Ha az n-edik k-szögszámot S n ( ) -val jelöljük, akkor
k
1
2
n
S n ( ) = (k − 2)H − (k − 3) , vagyis S n ( ) = [(k − 2)n − (k − 4) ] ahol
k
k
n
n
2
, k n   , n  3 .
1 ( n n + 1)
2
Tehát az n-edik 3-szög szám képlete: S n (3) = (n + ) n = , az n-edik
2 2
1
2
4-szögszámé S (4) = 2n = 2 n , az n-edik ötszögszámé
n
2
1 n (3n − 1)
2
S (5) = (3n − ) n = , az n-edik hatszögszámé pedig
n
2 2
1
2
S (6) = (4n − 2 ) = n (2n − és így tovább. A sokszögszámoknak van
1)
n
n
2

33