Page 151 - vol2


kerülete, akkor k  n K  K , és mivel limk = lim K = 2 R , ezért
n
n→ n n→ n
K = 2 R .

Megjegyzés: Teljesen hasonlóan bizonyítható a kör területszámolási
képlete is, T = R .
2
2
  →
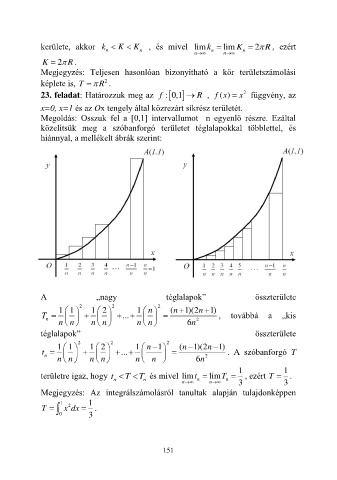
23. feladat: Határozzuk meg az f : 0,1 R , ( )f x = x függvény, az
x=0, x=1 és az Ox tengely által közrezárt síkrész területét.
Megoldás: Osszuk fel a [0,1] intervallumot n egyenlő részre. Ezáltal
közelítsük meg a szóbanforgó területet téglalapokkal többlettel, és
hiánnyal, a mellékelt ábrák szerint:

A „nagy téglalapok” összterülete

1 1  2 1 2  2 1 n  2 (n + 1)(2n + 1)


T =   +   + ...+   = , továbbá a „kis
n



n n  n n  n n  6n 2
téglalapok” összterülete
1 1  2 1 2  2 1 n −  2 (n − 1)(2n − 1)
1



t =   +   + ...+   = . A szóbanforgó T
n
n n  n n  n  n  6n 2


1 1
területre igaz, hogy t  n T T és mivel limt = n→ n limT = n→ n 3 , ezért T = .

n
3
Megjegyzés: Az integrálszámolásról tanultak alapján tulajdonképpen
T =  0 1 x dx = 2 1 .
3
151