Page 103 - vol1

A bejárhatósági problémák egy érdekes osztályát képezik azok, amelyeknél
például egy épület alaprajza szerint kell ajtókon áthaladni.

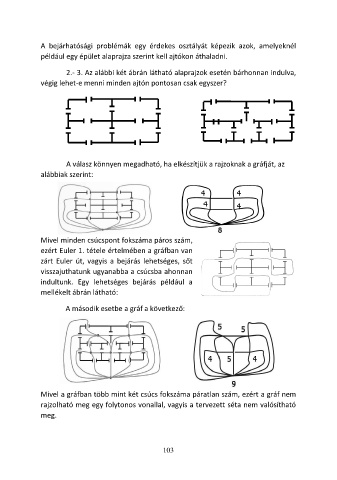
2.- 3. Az alábbi két ábrán látható alaprajzok esetén bárhonnan indulva,
végig lehet-e menni minden ajtón pontosan csak egyszer?

A válasz könnyen megadható, ha elkészítjük a rajzoknak a gráfját, az
alábbiak szerint:

Mivel minden csúcspont fokszáma páros szám,
ezért Euler 1. tétele értelmében a gráfban van
zárt Euler út, vagyis a bejárás lehetséges, sőt
visszajuthatunk ugyanabba a csúcsba ahonnan
indultunk. Egy lehetséges bejárás például a
mellékelt ábrán látható:

A második esetbe a gráf a következő:

Mivel a gráfban több mint két csúcs fokszáma páratlan szám, ezért a gráf nem
rajzolható meg egy folytonos vonallal, vagyis a tervezett séta nem valósítható
meg.

103